Chapter 11 Matched T Test

11.1 Theory

When both sample means were produced by the same participants, we conduct what is known as a dependent-samplestest. This is a test of the average difference between the scores in one condition and the scores in another condition—thus, the unit of measurement is a difference score.

\(\bar{D}=\Sigma D /n\) \(D= X_{i1} - X_{i2}\)

The mean of this sampling distribution is \(\delta\)= 0. The shape of this sampling distribution is approximately normal. The standard error of the sampling distribution of mean difference scores is

\(s_{\bar{D}} = \frac{s_D}{\sqrt{n}}\)

\(s_d = \sqrt{\frac{\Sigma{(D-\bar{D})^2}}{n-1}}\)

The test statistic is

\(t = \frac{\bar{D}-\delta}{s_{\bar{D}}}\) \(s_\bar{D} =\frac{s_D}{\sqrt{n}}\)

The effect size is calculated

\(d =\frac{\bar{D}}{S_D}\)

\(S_d = \sqrt{\frac{\Sigma{(D-\bar{D})^2}}{n-1}}\)

You are investigating whether the older or younger male in a pair of brothers tends to be more extroverted. So you test where each one falls on an introversion-extroversion scale. The results are as follows:

# Dep
younger <- c(10,11,18,12, 15)
older <- c(18,17,19,16,15)
dep <- data.frame(younger, older)

Step one: State the null and alternative hypotheses

\(H_o : \delta = \mu_1 - \mu_2 = 0\) \(H_a : \delta = \mu_1 - \mu_2 != 0\)

Step two: Set the criterion for rejecting H0. Alpha is usually set to .05, but could be other values depending on the research context. Make sure you’ve considered directionality!

Step three: Select the sample and collect your data.

Step four: Locate the region of rejection and critical values.

\(t_{cv,dv=4, \alpha=.05}= +/- 2.77\)

Step five: Compute the appropriate statistic. We were never given \(\sigma\)or \(\sigma^2\), so we use the t test.

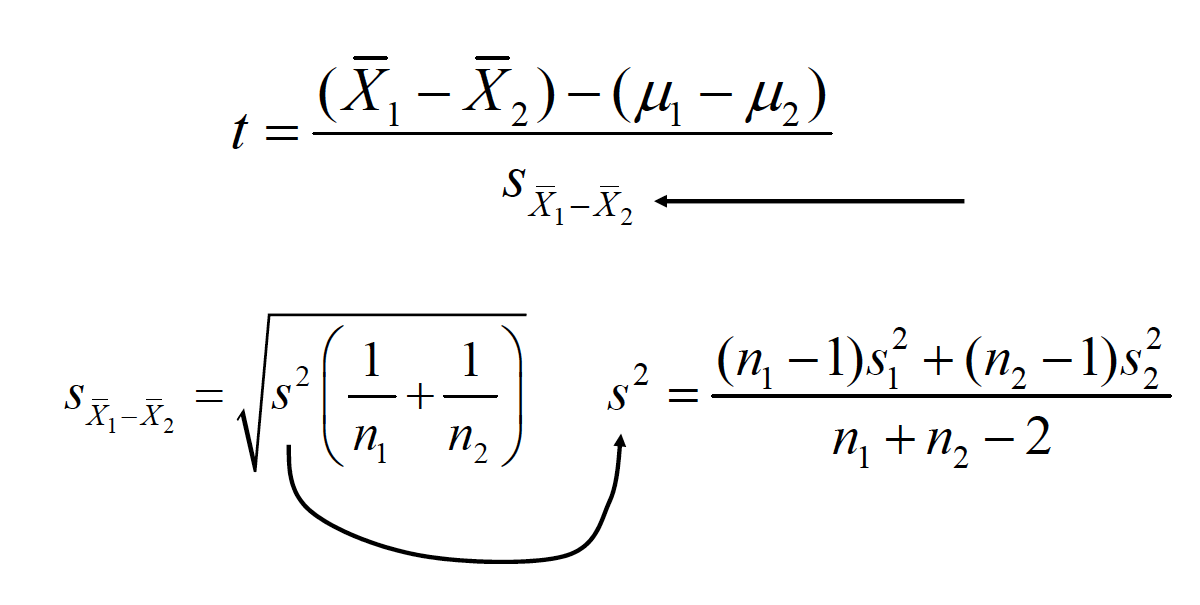
Convert me

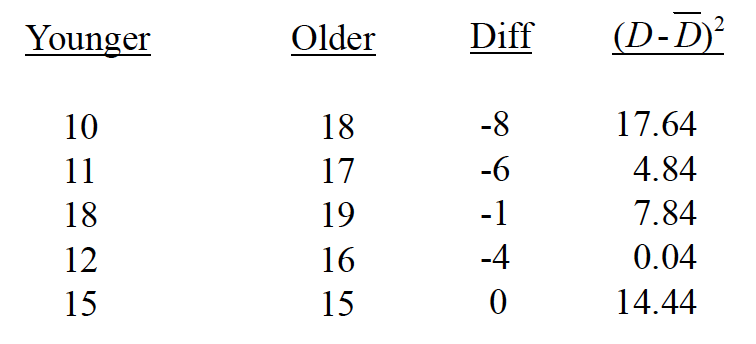
Convert me

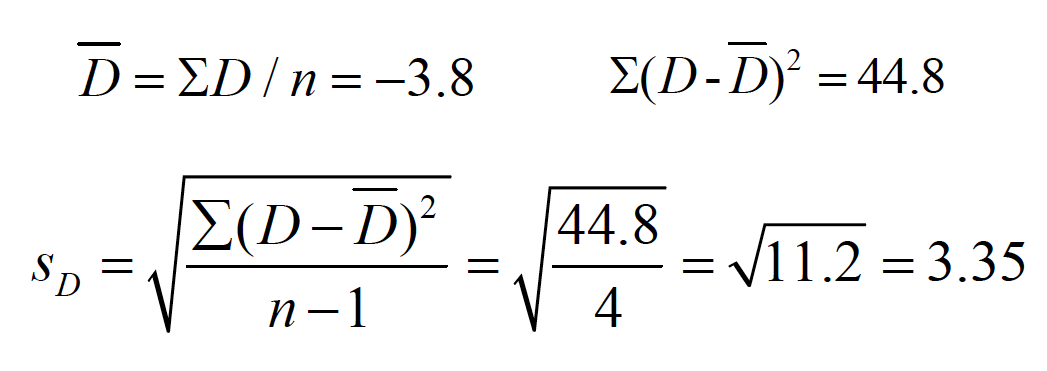
Convert me

\(s_D=3.55\) \(s_\bar{D} =\frac{s_D}{\sqrt{n}}= \frac{3.35}{\sqrt{5}}\)

\(t = \frac{\bar{D}-\delta}{s_\bar{D}} = \frac{-3.8-0}{1.50}= -2.53\)

Step six: Decide whether to reject H0. Is -2.53 more extreme than the critical value?

\(t_{cv,dv=4, \alpha=.05}= +/- 2.77\)

“The average extroversion value for the younger male siblings (M= 13.2) did not differ significantly from the extroversion value for the older siblings (M= 17.0), t(4) = 2.53, p> .05.”

Effect size computation

\(d = \frac{\bar{D}}{s_D}= \frac{-3.8}{3.35} = -1.13\)

Small: = 0.25Medium: = 0.50Large: = 1.0

“The average extroversion value for the younger male siblings (M= 13.2) did not differ significantly from the extroversion value for the older siblings (M= 17.0), t(4) = 2.53, p> .05, Cohen’s d= 1.13.”

So, why does the effect size calculation disagree with the result of the hypothesis test?

Template file