Chapter 16 Factorial Designs with Repeated Measures

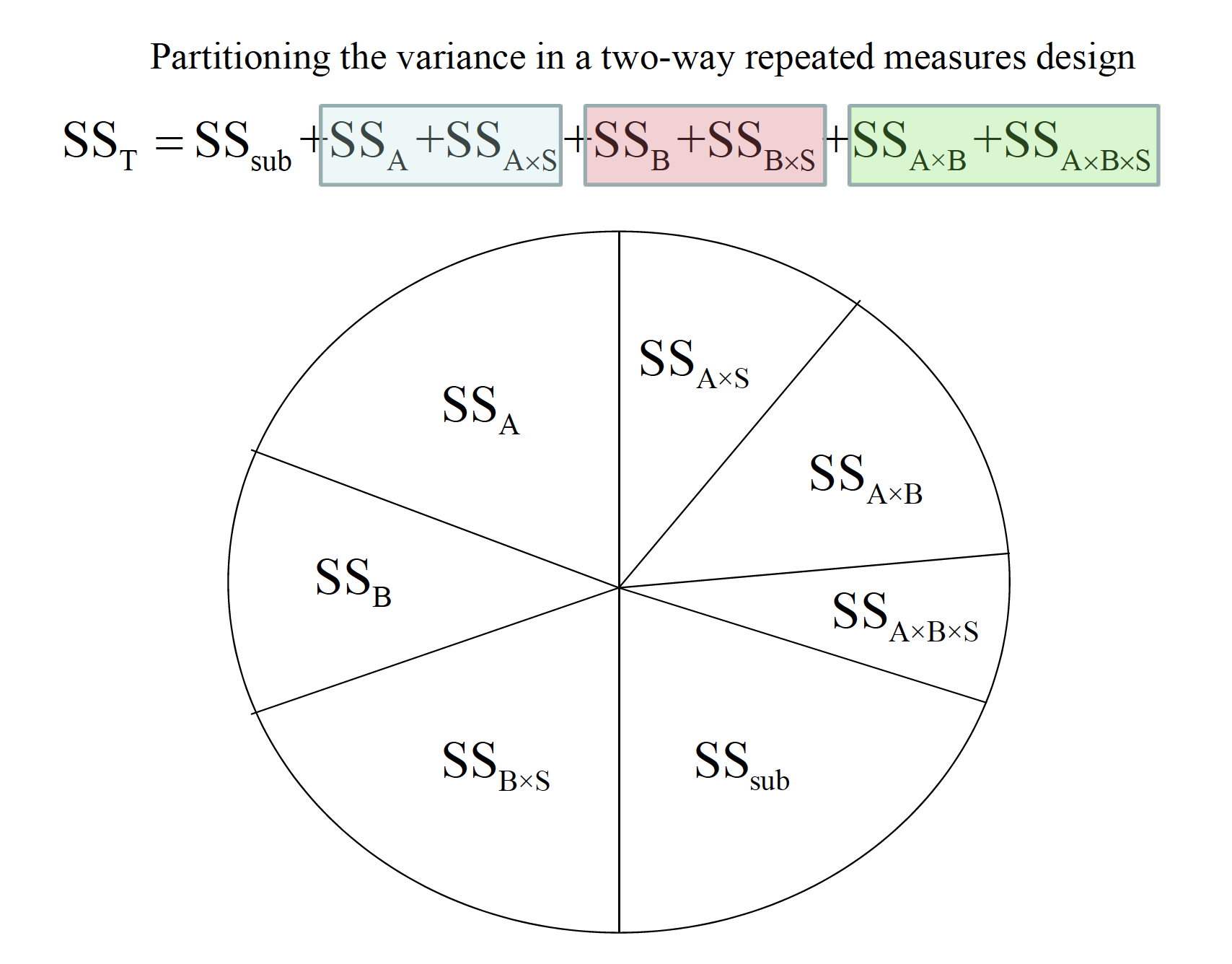
1. The partitioning of variance when all factors are repeated measures includes multiple subject × treatment interactions.
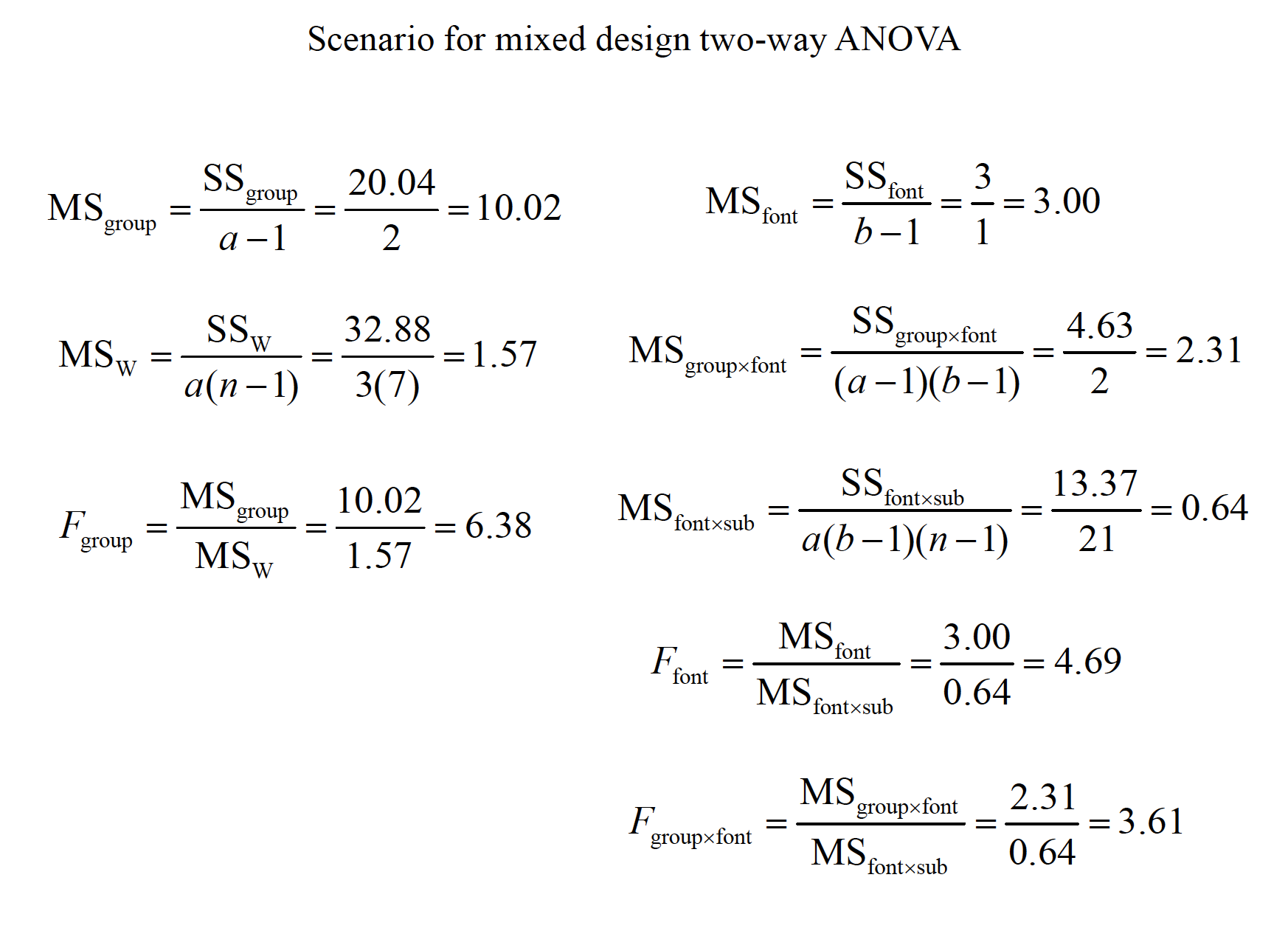
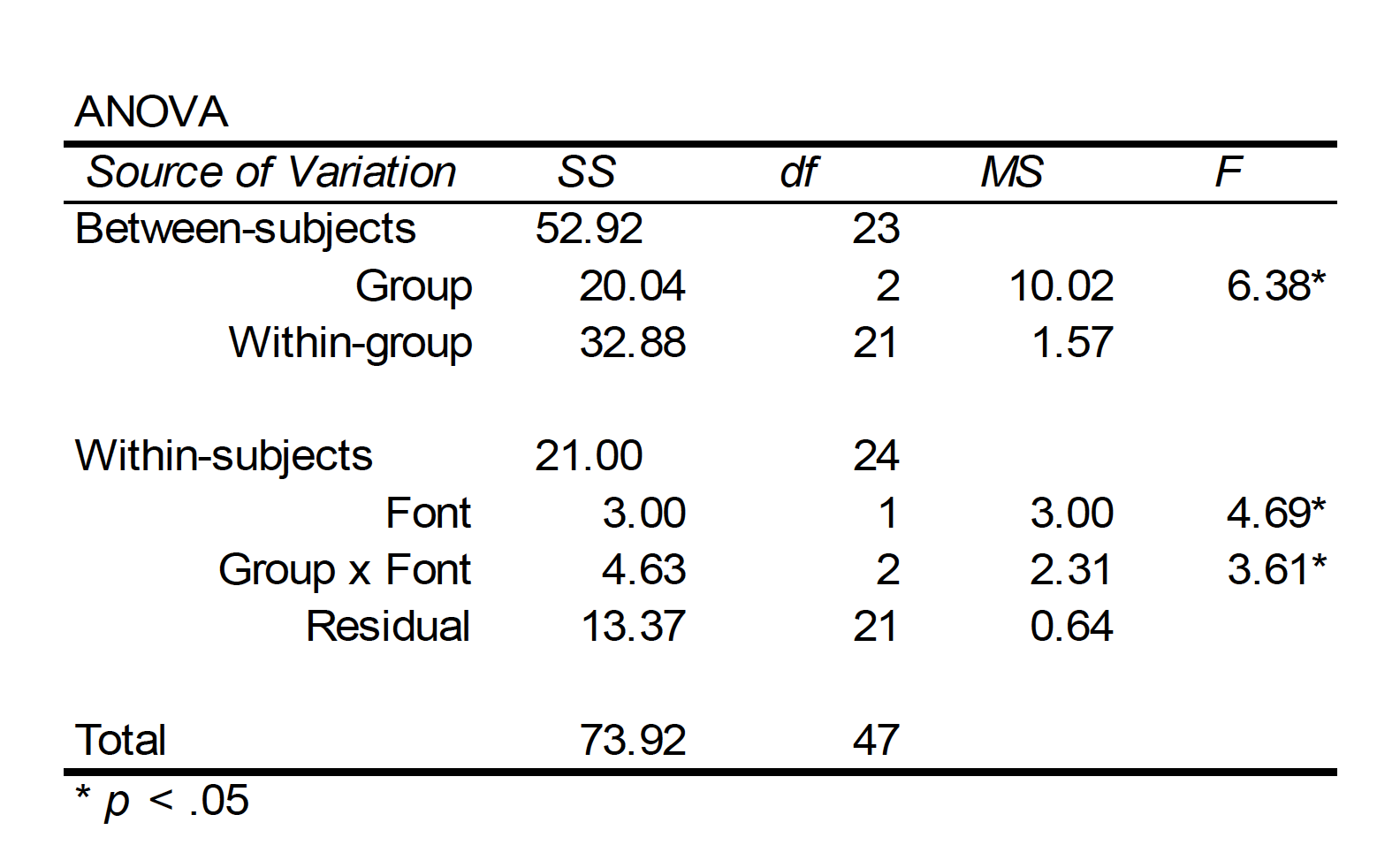
2. A full computational example of a mixed design with one repeated measures factor and one between-subjects factor.
3. The assumptions of designs with repeated measures

In cases where both (or more) factors are repeated measures, each main effect and interaction is generated as usual, but each error term consists of some type of interaction with subjects.

fdrm

fdrm

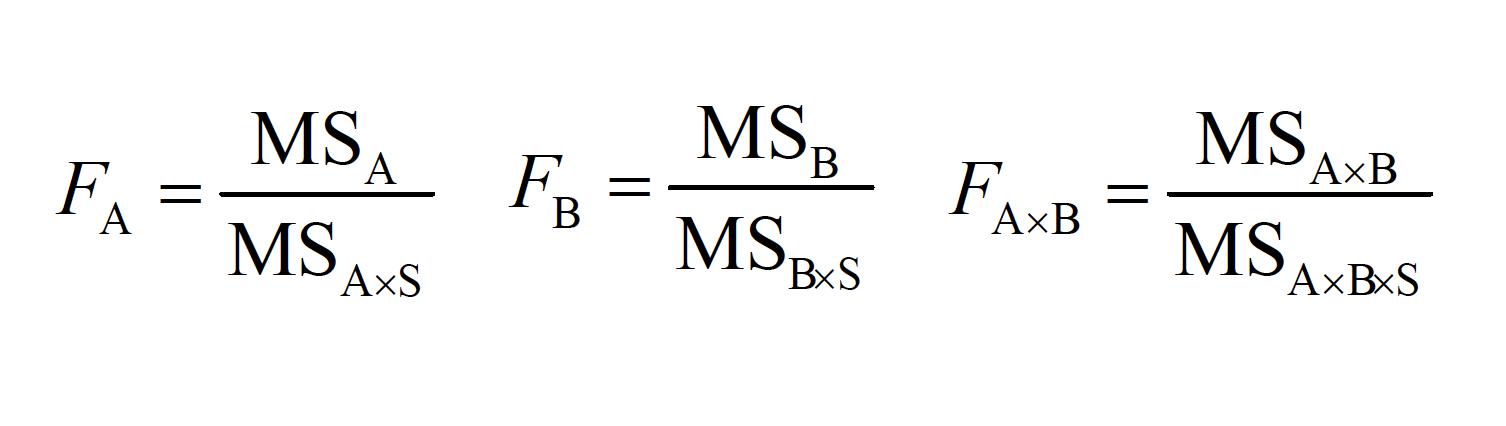
fdrm

In cases where at least one factors us repeated measures and at least one other is between subjects, we have a mixed design. The sources of variation in a two-way mixed design are below:

fdrm

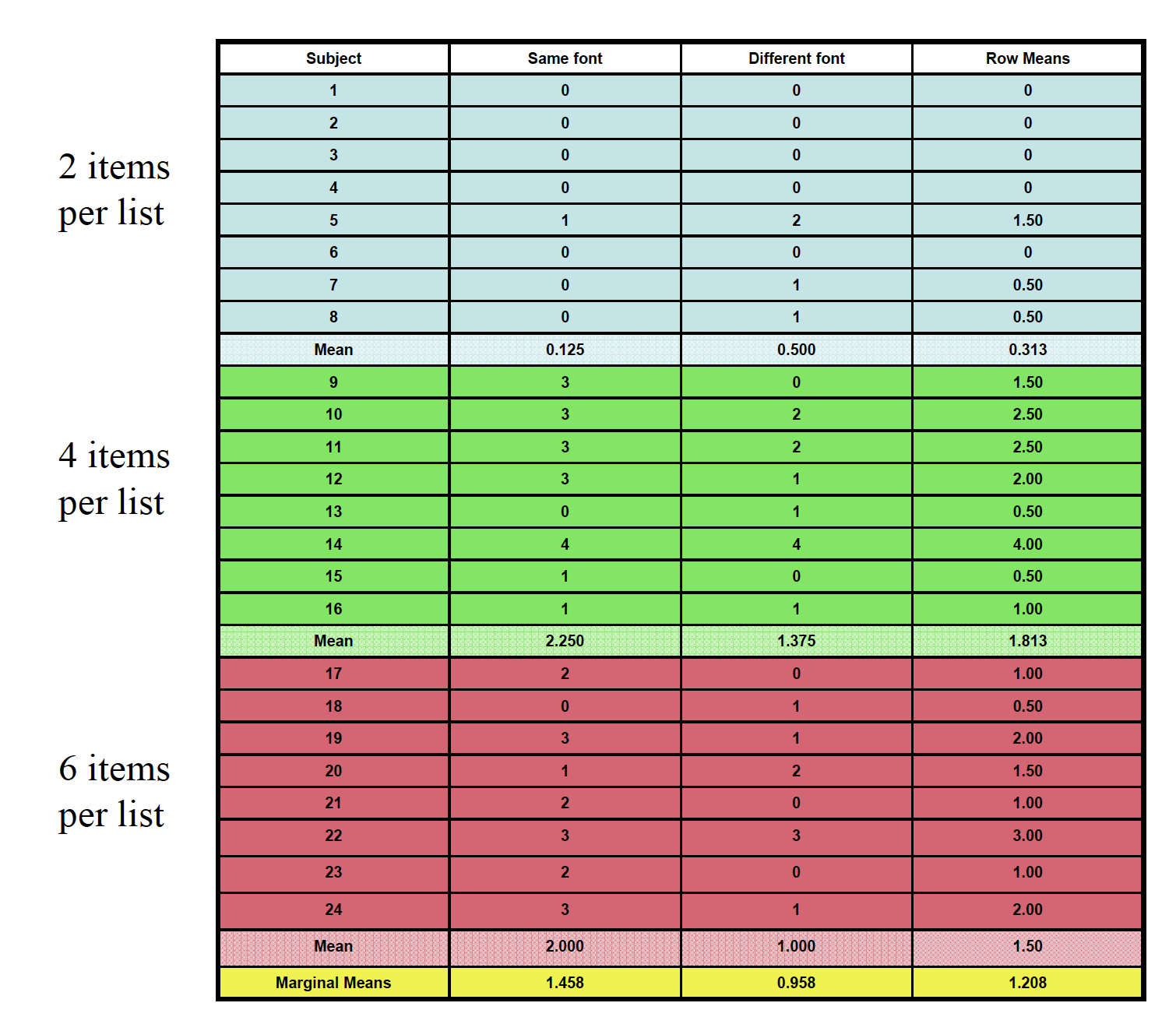
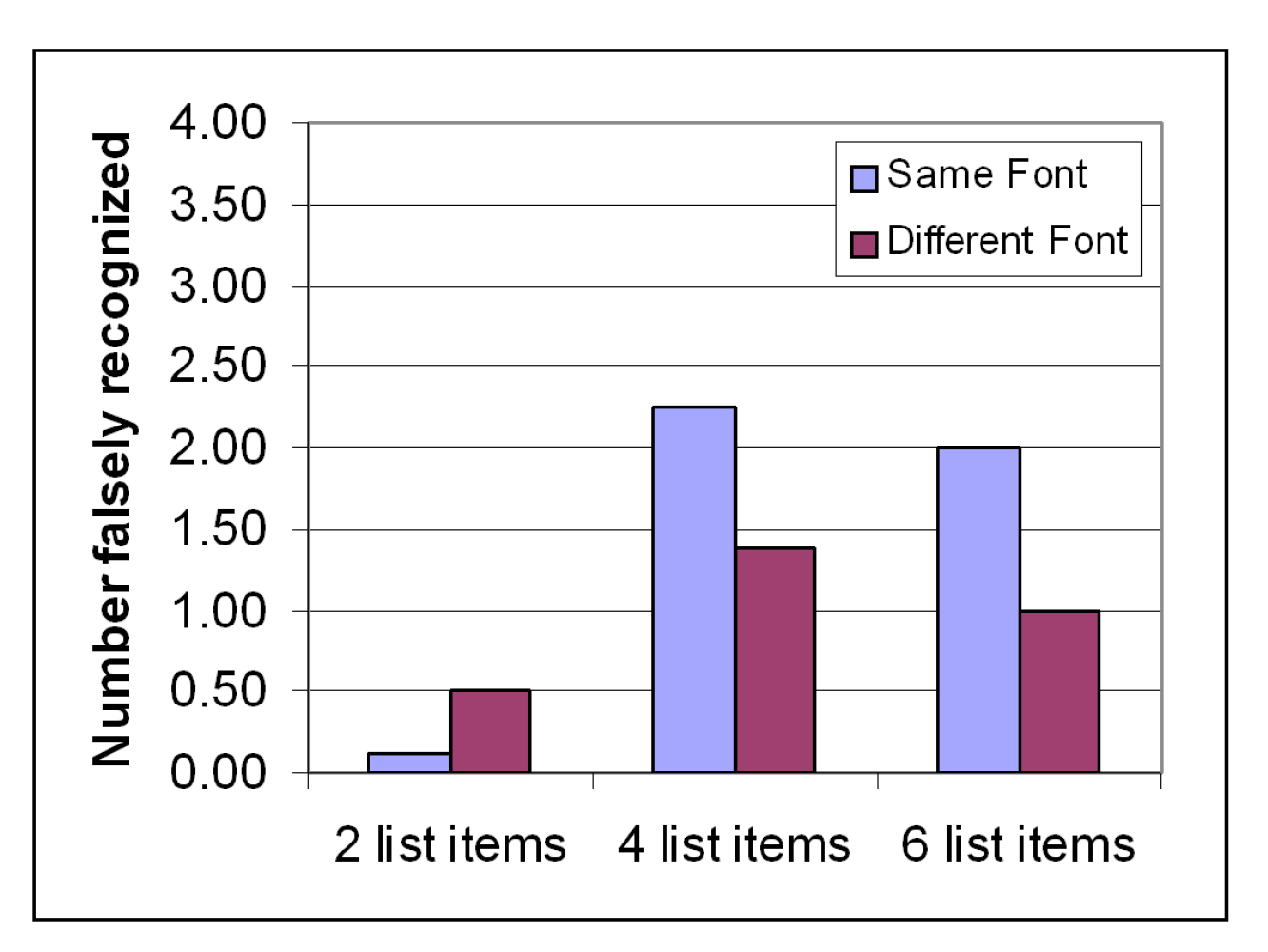
A memory psychologist is interested in how false memories are affected by changes in context. Three groups of people were asked to learn lists of words connected to a missing theme. For example, the words BED, REST, PILLOW, BLANKET, NIGHT, & SLUMBERare all related to SLEEP. Group 1 studied many lists like these, with only the first two items for each list (e.g., only BED and REST). Group 2 studied the same lists, but including the first 4 items per list. Group 3 studied the same lists, but including all 6 items in each. Each list had a very distinctive font, as I used above. Each group then got a memory test. Included on this memory test were the “missing” theme items, such as SLEEP. Sometimes the theme items were in the same font as their list mates (e.g., SLEEP). Other times, these items were presented in a different font (e.g., SLEEP). There were 4 items in each of these test conditions. The data presented on the next slide represent how many, out of 4, of these missing theme items were called “old” on the memory test. These are, therefore, false memories. The question is whether the factors of list length and font style at test affect how many of these occur.

fdrm

fdrm

In cases where at least one factors us repeated measures and at least one other is between subjects, we have a mixed design. The sources of variation in a two-way mixed design are below:

fdrm

fdrm

16.1 Assumptions of Mixed ANOVA

1. Sample randomly selected from the population
2. The DV is normally distributed in the population
3. The variances of difference scores from all possible pairs of conditions are equal and the covariances(or correlations) between pairs of conditions are equal (sphericityor circularity). 4.These covariance structures, or matrices, are equal across the between- subject groups in the study (i.e., for each list length condition).

16.1.1 Equal Variance

– Run Leven’s Test and Box’s

Yuck! We don’t have equal variances for the ‘same font’ scores among our conditions. Nor do we have equal covariance structures across our 3 list length conditions (Box’s test).

Basically, then, we shouldn’tuse a pooled error term for any post-hoc comparisons. One plan could be to run two separate one-way ANOVAs across condition to assess simple main effects, and checking the Welch’s and Brown-Forsythe ANOVA options for each. We should apply a Bonferronicorrection for any of these post-hoc comparisons.

16.1.2 Simple Main Effects

Even with a Bonferronicorrection (.05/2), there are group differences for same font condition, but not for the different font condition. We could then perform a Tukeytest for the pairwisedifferences for the same font condition (i.e., simple comparison).